国語編はこちらです。
コロナウイルスが本格化してきて、家での仕事ばかりになってきました。
入試問題解いているだけで仕事になるので、それはそれでいいですけどね。
数学編です。
実際の問題やデータを参照しながらやっていこうと思いますよ。
平成30年のデータを使ってやっていきます。
平均点は58点
まあ、普通です。60点を目安に作られていますからね。
数学はやや低めになることが多いので、そういう意味でも非常に普通の点数ですね。
単元、配点、平均正答率
正答率についてはあとで触れていきますね。
配点は大問１～３までは全て５点。
４の記号は２点、証明が６点
５は数値が３点、説明が４点、最後が５点です。
まあ、概ね５点と考えていいですね。
大問ごとの分析
大問１
計算問題です。
正答率は９７％～７４％。
すべての問題が、４人中３人は正解するレベルの問題です。
まず、受験生が行うべきことは、この大問１の全問正解です。
ここは、全問正解以外ありません。
私なら、ここが全問正解できるまで次の大問は行かせません。
全問正解とは、6/6ではありません。少なくとも100/100、できれば1000/1000です。
ちなみに、(6)のように解の公式を利用した因数分解を２回に１回は出題しているので、
絶対に解の公式は暗記しておきましょう。まあ、塾生ならできるまで補習ですから、覚えてない人なんていないでしょうけど。
大問２
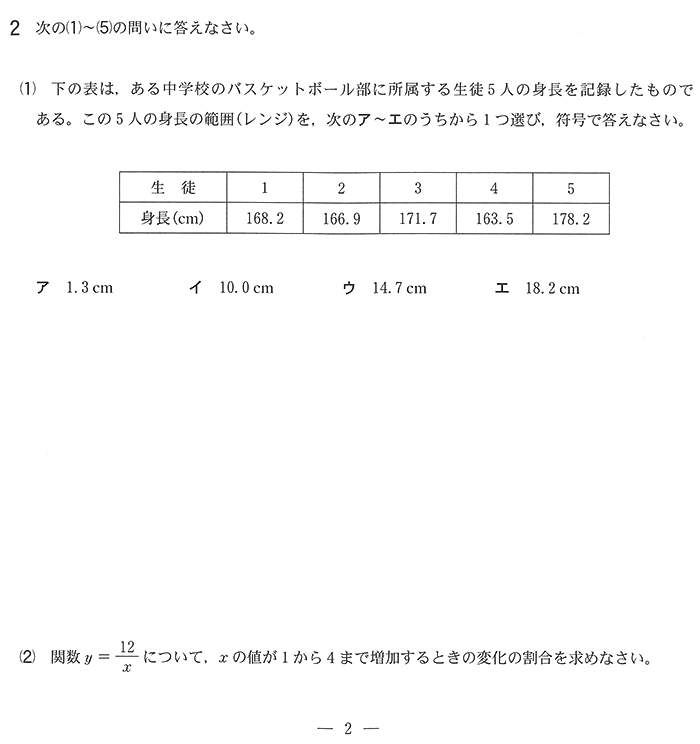
正答率（１）７７％
ヒストグラムですね。昭和生まれは見慣れない問題ですよね。私も学校で習ってません。ただし、千葉では毎年必ず出ています。
正答率（２）４５％
反比例の変化の割合を答えるだけ・・・半分解けてないとか頭抱えちゃいます。
このレベルで半分間違ってくれるなら、戦わせやすいですけどね。
（３）６１％
簡単な１次方程式
（４）４２％
簡単な場合分けの問題ですね。半分解けないって結構ヤバイですよ。。。
多分、日本語が読めてないですよね。読解力の問題ですよ。
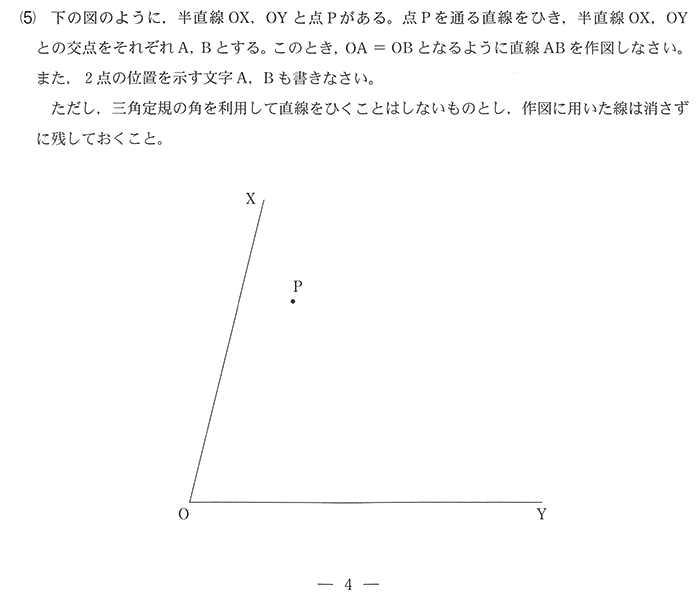
正答率は
（５）２９％
毎年出る作図問題です。これぐらいはできるように作図は徹底しておく必要がありますね。
まあ、間違って１問まででしょう。
大問３
例年、大問３は関数が出ます。
（１）二次関数ですが、教科書の初問レベル。簡単ですね。
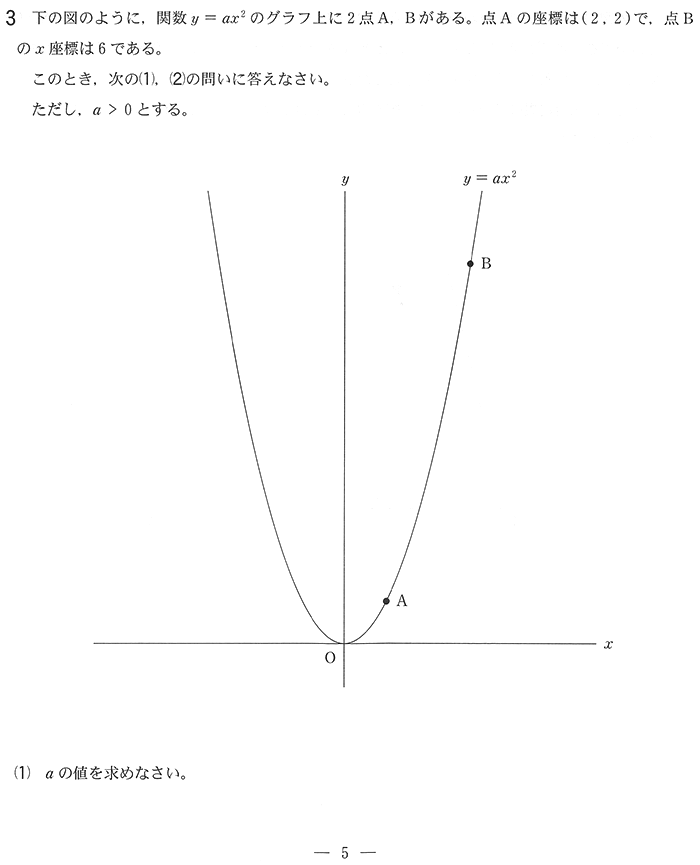
（２）関数の応用です。②が難しかったみたいですね。反対側に高さが同じになるよう作図するだけなんですが・・・
大問４
平面図形からです。大問４は伝統的に平面図形ですね。
相似の証明ですね。a,bは選ぶだけなんで無茶苦茶簡単です。
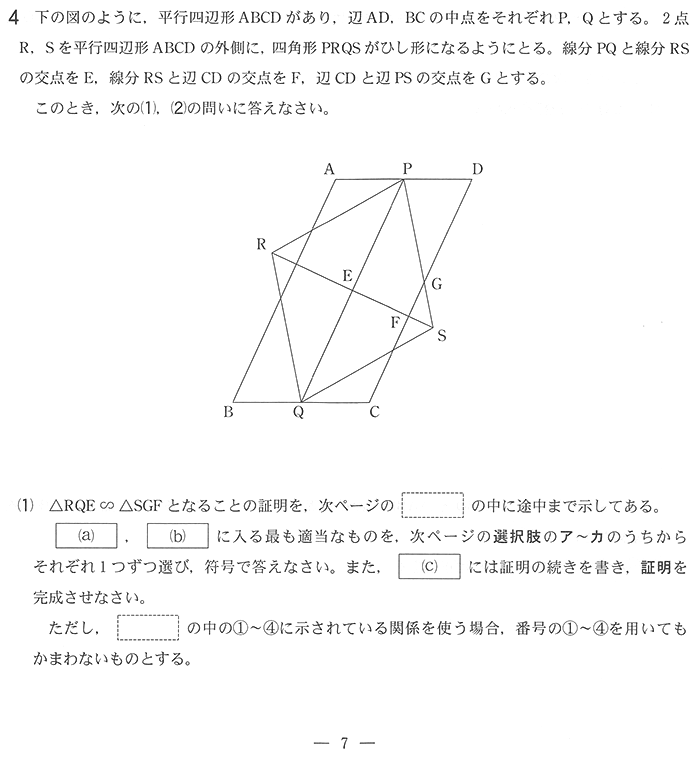
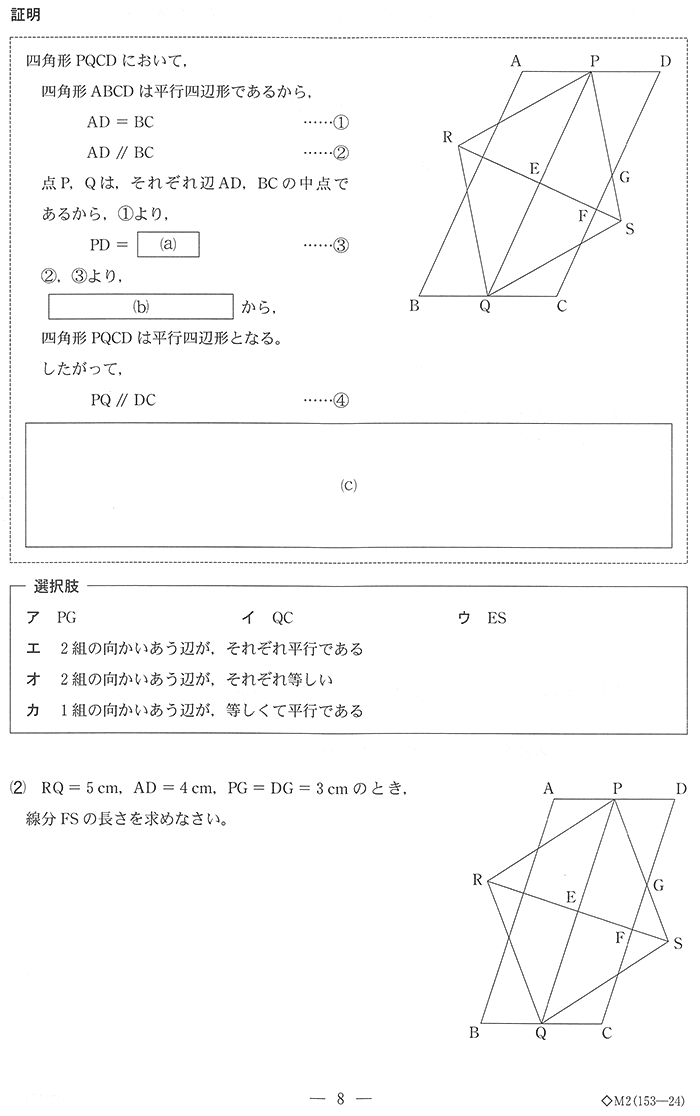
特に逆から導いていけば、わからなくても答えられますからね。確実に４点取りましょう。
問題はｃからですね。時間もかかりますし、無理に優先して解く必要はないと思います。
６点と、設問の中で一番高いですが、所詮、最初の５点と１点しか変わりません。
そして（２）に至っては、解くべきではないと言っていいでしょう。
（２）の正答率、0.2％です。0.2とは、500人に1人しか正解していないということです。
そして、この入試は県立船橋や、県立千葉中といった化物高校を受験する生徒も受けているんです。
500人にひとり、みなさんの学校の３年生の生徒数は何人ですか？
では、学校が３つあって一人しか解けない問題なんです。
あなたは、その一人の自信がありますか？
では、この問題を解かなくてもいいんですよ。
毎年こんなゲキムズ問題があるわけではないんですが、
８０点が目標なら
大問４の最終問題は捨てるつもりでほかを優先するのもアリです。
大問５
大問５は規則性が多いですが、この年は立体図形です。
まあどちらかが出ると思っておいていいと思います。
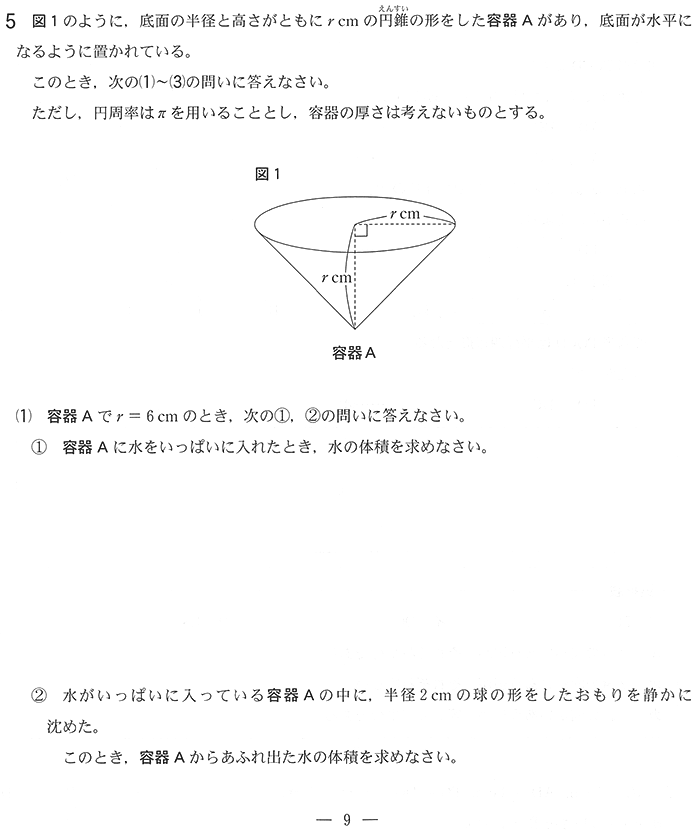
①は６３％。教科書初問レベル。②にしても３３％で、さっきの作図問題より正答率が高いんですね。
ここは、取りたいんです。
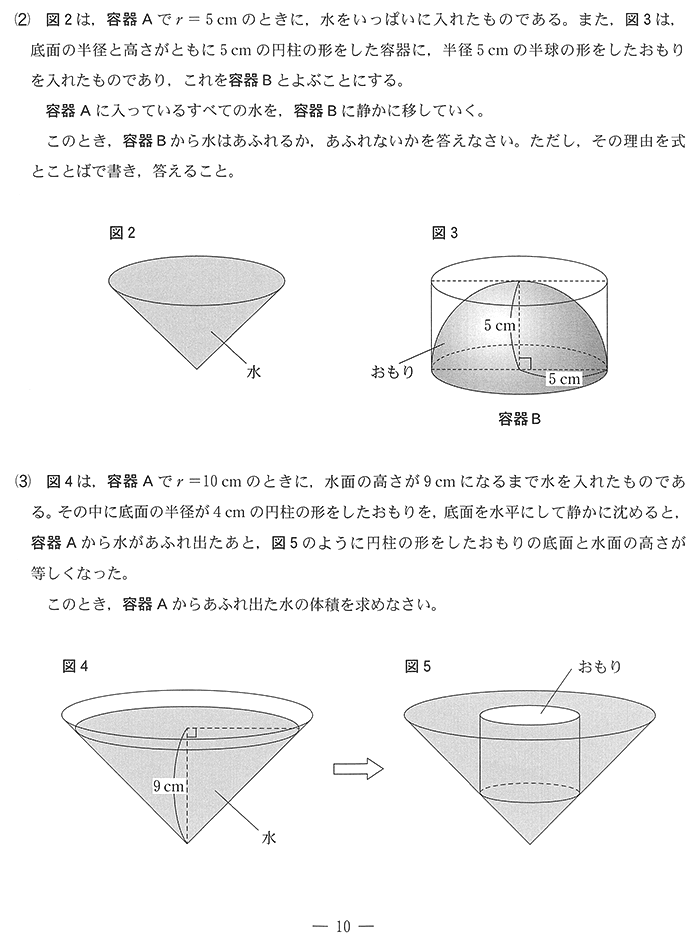
（２）は４点と少なめですが、正答率は１７％です。
（３）は７％です。数学が得意なら真横からの投影図を書けばすぐです。正解したいところですね。
対策方法
目標点数によってプランが変わってきます。
この年の問題を、正答率２５％以上の問題全てを正解した場合の得点は・・・
３０＋２５＋１０＋４＋６＝７５点です。
この年の７５点は、上出来だと思います。
内申にもよりますが、
うちが目標としている上位の津田沼や国分が大体５教科３５０点が目安ですからね。
平均は７０点。
得点しにくい数学で７５点は、上々なんですよ。
それでももう少し得点したい場合
正答率１割台の２問を正解しましょう。それで１０点増えて８５点です。
９０点を取るには、最終問題の７％をとって、ちょうど９０点です。
結論
数学は、簡単な問題を絶対間違えないように練習することが高得点を取る秘訣です。
難しい問題なんてね、どーせ授業で扱っても半分も頭に入ってないですから。
難しい問題なんて、「わかんない」って言っとけばいいんですもん。
一生懸命考えたふりして、「？」首をひねる。
先生から答え聞いて、写す。勉強終わり。
こんなの５分も勉強したことになりませんし。
これね、勉強してるのは解説考えてる先生だけのやつですよ。
最上位受ける意識高い子相手ならやりますけどね。
私はフツウの層にはこういうの無駄だと思ってるんで。
それよりも簡単な問題、ギリギリ自分だけでもできるレベルの問題
そういう問題を徹底的に伸ばしたほうが、脳は鍛えられるんですよ。
簡単な問題なら、「わかんない」はおかしい、
サボリと、頑張っている子と、違いがはっきり出ちゃう。
そしてなにより、基礎が完璧な人間だけが、応用・発展に進むのが物事の基本中の基本でしょう。
では、簡単な問題を確実に正解するために必要なこととは何でしょうか！？
答えは・・・
物量！！！！
物量！！！！！！
まあでも、ちんぷんかんぷんな問題１つやるより、自力でいけるギルギリをどんどんヤルほうが、絶対楽だし、楽しいですからね。
同じことばっかりやるの嫌いなのはわかってます。
そこをうまく続けさせるのが、こちらの仕事ですから、任せてください。
